I wanted to create more boards for my set and though about making a generator. There’s an awesome book – Mazes for Programmers by James Buck. I can’t recommend it enough if you want to learn how to generate mazes of any kind or shape. I played with that for a while, but I was still interested in how many possible boards there were. Eventually, I came up with a binary system for a square’s walls.

So that a square’s walls can be represented by number between 0 and 15.

To define a Wiz-War board we need twelve numbers. These can define ANY board.
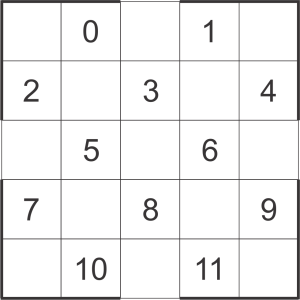
All squares against the sides can have three possibilities since one wall is already defined and I hate corner dead ends. Let’s say all the inner squares need at least one wall so:
| Squares | Wall Options |
|---|---|
| 0, 2 | {0, 1, 2} |
| 1, 4 | {0, 1, 8} |
| 7, 10 | {0, 2, 4} |
| 9, 11 | {0, 4, 8} |
| 3, 5, 6, 8 | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14} |
So the number of combinations is $3^8 * 14^4 = 252,047,376$. We require all squares to be accessible from any other square. If we remove all those (and all boards with less than ten walls), we’re left with 88,460,134 possible boards in a 2G file.
I hate dead ends on a board that are not on a treasure square. There is no reason for any moveable character to go there unless forced. It essentially becomes a dead square. The stats go like:
| dead ends | # of boards |
|---|---|
| 0 | 19,334,474 |
| 1 | 32,399,364 |
| 2 | 23,828,184 |
| 3 | 9,935,257 |
| 4 | 2,547,512 |
| 5 | 385,776 |
| 6 | 29,568 |
Something I call a “four” is a two-by-two square without any walls within it. We don’t want too much open space on a board. The stats go like:
| fours | # of boards |
|---|---|
| 0 | 6,170,684 |
| 1 | 18,605,068 |
| 2 | 25,830,988 |
| 3 | 21,692,876 |
| 4 | 11,743,626 |
| 5 | 3,840,560 |
| 6 | 576,332 |
So if we remove all boards with more than one non-treasure dead end and more than one “four,” we end up with 11,444,356 boards in a 273M file. Much more manageable.
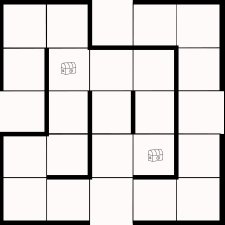
Now we can deal with rotations. Some of the boards will be represented four times in the data file because of 90-degree rotations. The following boards will be in the file. They are all rotations of each other.
 |
 |
 |
 |
| (1,1,2,5,8,8,1 4,5,8,4,8) | (2 1,2,4,8,10,10,4,8,8,4,4) | (2,1,2,5,1,4,2 2,5,8,4,4) | (1,1,2,2,1,10,10,2,1,8,4,8) |
Because of the placement of treasure squares, we can easily drop all 180-degree rotations. This is computationally expensive which is why I reduced the size by other means first. There are 810 boards that are rotations of themselves and 5,721,773 boards that are rotations of another board. Pulling the duplicates out we get a 136M file of 5,722,583 boards.
This data is manageable to put into a program, so that rather than generating a board, you just pick one. The numbers in the upper left of each square are ‘breadcrumbs’. It’s the number of movement points needed to get from the center to that square. That’s so you can place doors for the board’s player to access in fewer moves. In the next example, I’d put a door on a wall next to that ’14’ square.
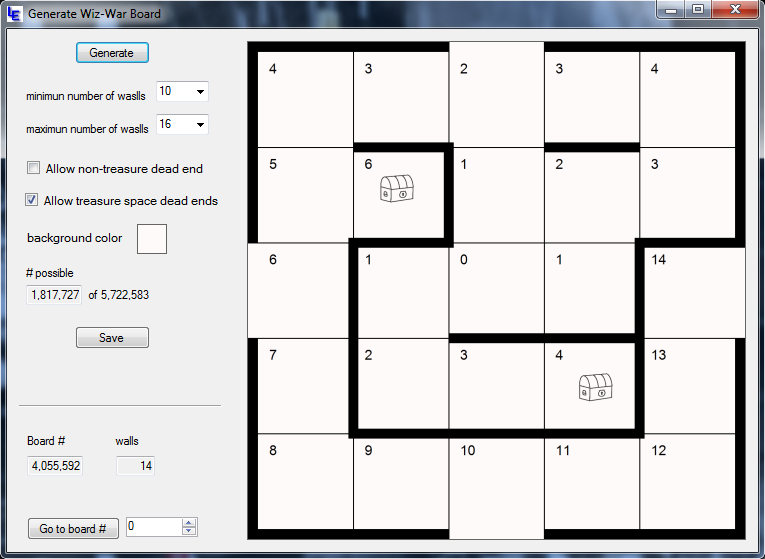
Give the program a few seconds to start up because it has to load the data. It takes five or six on my i7 processor.
 |
Download my Wiz-War Board Generator – 15.1M MD5 for zip – 99570fbfcba026ad155c119e4c88fcc1 |
Legal crap (O brave new world that has such people in it.):
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
